Understanding Wavelets

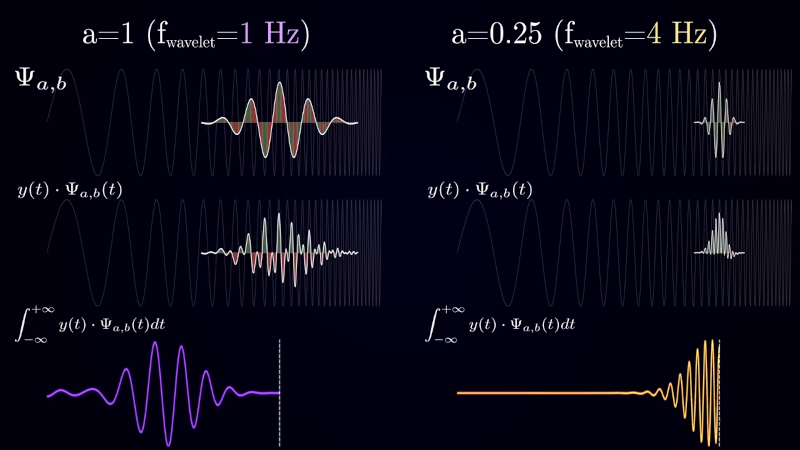
Mathematical transforms can be a great help in understanding signals. Imaging trying to look at a complex waveform and figuring out the frequency components without the Fourier transform. [Artem Kirsanov] calls the wavelet transform a “mathematical microscope” and his video gives you a great introduction to the topic. You can see the video below.

The video starts with a discussion about how the time domain and frequency domain have a dual relationship — not big news if you’ve dealt with Fourier transforms and — in fact — that’s the next topic in the video. However, there are limitations to the transformation — you lose time domain information in the process.

Obviously, the wavelet transform can address these limitations. The transform is similar to applying Fourier, but instead of decomposing to a series of infinite sine waves, wavelet transformation decomposes signals into finite functions that meet certain conditions.

You do need a little math to follow the video, but probably not as much as you might think. The explanations are clear and there are few assumptions about your prior knowledge. If you’ve encountered windows in Fourier analysis, the ideas are somewhat similar.

If you want to experiment with some DSP concepts in a spreadsheet, you can do that. If you don’t intuitively grasp the Fourier transform, try watching [3blue1brown’s] enlightening video on the topic.