Our Favorite Things: Binary Search

You might not think that it would be possible to have a favorite optimization algorithm, but I do. And if you’re well-versed in the mathematical art of hill climbing, you might be surprised that my choice doesn’t even involve taking any derivatives. That’s not to say that I don’t love Newton’s method, because I do, but it’s just not as widely applicable as the good old binary search. And this is definitely a tool you should have in your toolbox, too.
Those of you out there who slept through calculus class probably already have drooping eyelids, so I’ll give you a real-world binary search example. Suppose you’re cropping an image for publication on Hackaday. To find the best width for the particular image, you start off with a crop that’s too thin and one that’s too wide. Start with an initial guess that’s halfway between the edges. If this first guess is too wide, you split the difference again between the current guess and the thinnest width. Updated to this new guess, you split the differences again.
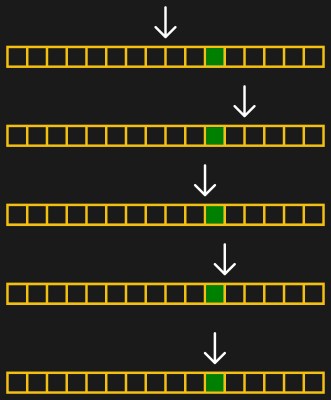 But let’s make this even more concrete: an image that’s 1200 pixels wide. It can’t get wider than 1200 or thinner than 0. So our first guess is 600. That’s too thin, so we guess 800 — halfway between 600 and the upper limit of 1200. That ends up too wide, so we next guess 700, halfway between 600 and 800. A couple more iterations get us to 650, 675, and 688. In this case, we got down to the pixel level pretty darn fast, and we’re done. In general, you can stop when you’re happy, or have reached any precision goal.
But let’s make this even more concrete: an image that’s 1200 pixels wide. It can’t get wider than 1200 or thinner than 0. So our first guess is 600. That’s too thin, so we guess 800 — halfway between 600 and the upper limit of 1200. That ends up too wide, so we next guess 700, halfway between 600 and 800. A couple more iterations get us to 650, 675, and 688. In this case, we got down to the pixel level pretty darn fast, and we’re done. In general, you can stop when you’re happy, or have reached any precision goal.
What’s fantastic about binary search is how little it demands of you. Unlike fancier optimization methods, you don’t need any derivatives. Heck, you don’t even really need to evaluate the function any more precisely than “too little, too much”, and that’s really helpful for the kind of Goldilocks-y photograph cropping example above, but it’s also extremely useful in the digital world as well. Comparators make exactly these kinds of decisions in the analog voltage world, and you’ve probably noticed the word “binary” in binary search. But binary search isn’t just useful inside silicon.
Why Can’t I Beat It?
That example of cropping photographs above was no joke. I follow that exact procedure multiple times per day. Or at least I try to. When I’m carrying out a binary search like this in my head, it’s incredibly hard to discipline myself to cut the search space strictly in half each time. But I probably should.
 My son and I were calibrating a turtle bot a few weeks back. Basically, we needed to figure out the magic PWM percentage that made two different DC motors spin at the same speed. This would have been a perfect application of binary search: it turned either slightly to the left or the right, and we had good bounding PWM values for each case. But we kept saying, “it’s only going a little to the left” and bumping the PWM up by tiny increments each time. After repeating this five times, it was clear to me that we should have been using a binary search.
My son and I were calibrating a turtle bot a few weeks back. Basically, we needed to figure out the magic PWM percentage that made two different DC motors spin at the same speed. This would have been a perfect application of binary search: it turned either slightly to the left or the right, and we had good bounding PWM values for each case. But we kept saying, “it’s only going a little to the left” and bumping the PWM up by tiny increments each time. After repeating this five times, it was clear to me that we should have been using a binary search.
To see why you probably shouldn’t cheat on your binary searches, imagine that you don’t know anything more than that the goal is between the top and bottom values, but you’ve got this hunch that it’s closer to the bottom. So instead of picking the midpoint, you pick 10%. If you’re right, your next guess is going to be inside range that’s 10% of the current range, which is awesome, but if the target is even just a little bit bigger than 10%, you’re looking at a huge search space next round. Nine times bigger, to be exact. And the more uncertain you are about where the truth lies, the more likely you are to make a bad guess because there’s more space on the side that you’re betting against.
The choice of the midpoint isn’t arbitrary, and the above intuition can be given mathematical rigor (mortis) to prove that the midpoint is optimal when you don’t have extra information, but at the same time it’s incredibly hard for us humans to resist gambling. Take my son with the PWMs — he knew he was really close. But what he didn’t know was how close. Humans fixate on the current value. We “anchor“, in the terms of negotiations.
Part of why I love binary search is that this discipline helps beat down this human decision bias. But the other reason I love binary search is how readily it’s implemented in silicon.
Not Just a Lifehack
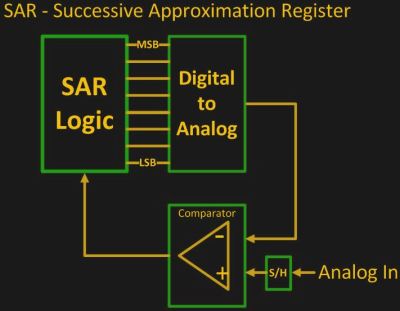 Those of you of a more software bent probably already have a deep love for binary search trees, but I’m a hardware guy. The analog to digital converters (ADCs) in my favorite microcontrollers all use binary search under the hood. They start out with the premise that the voltage they’re digitizing is between
Those of you of a more software bent probably already have a deep love for binary search trees, but I’m a hardware guy. The analog to digital converters (ADCs) in my favorite microcontrollers all use binary search under the hood. They start out with the premise that the voltage they’re digitizing is between GND and VCC.
Internally, the input voltage is stored on a sample-and-hold capacitor that’s connected to a comparator. The other input to the comparator takes the output of, ironically, a digital to analog converter (DAC). This DAC starts out with the midpoint voltage, VCC/2, and the comparator says whether the input is higher or lower.
With a 10-bit DAC, you can do this ten times, and that gives you a ten-bit ADC result. The coolest part is that the binary value on the ADC just falls out of the process. The first choice is the most-significant bit, and so on. If you’d like to see the circuitry in action, check out [Mitsuru Yamada]’s IC-based demonstrator. For more on ADCs in general, watch Bil Herd’s video.
Twenty Questions is Too Many
That’s why binary search is one of my favorite things. It’s a tool-slash-algorithm that I use multiple times per day, and it’s what underlies ADCs. Each step gets you essentially an extra bit worth of resolution, so in many real-world situations, you’re not likely to take more than 12 steps or so. Pick a number between 0 and 1,000 and I’ll guess it in ten tries.
As my photo-cropping example shows, you don’t even need to have a computable objective function, just the ability to say “bigger” or “smaller”. And where you do have an objective function, the computation burden is exceptionally light.
Of course there’s a time and a place for more complicated optimization routines — there are entire branches of science based on refining that particular mousetrap — but you’re not running simulated annealing in your head, or implementing it in raw silicon. The beauty of the binary search is that it’s also the simplest algorithm that could possibly work, and it works marvelously well for simple problems. Solving simple problems simply makes me smile.
Post a Comment